Vektörler

Çarpışma algılama(collision detection), ışıklandırma(lighting) gibi işlemleri anlayabilmek için öncelikle vektör, düzlem, normal gibi kavramları anlamak gerekir.

3 boyutlu uzayda bir nokta (x, y, z) koordinatlarıyla gösterilir. Bazen (x, y, z, w) olarak da gösterilebilir. Burada w orandır ve bunu (x, y, z) koordinatlarına dönüştürmek için (x/w, y/w, z/w) işlemini yapmamız gerekir. Noktalar bir poligonun köşelerini, yada bir ışığın pozisyonunu tanımlamak gibi işlemlerde kullanılabilir.

Vektörlerde bir nokta ile tanımlanabilir. Ama bir vektörün asıl gösterdiği şey bir doğrultudur.

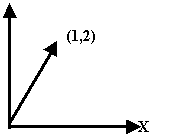
1. Vektörler Üzerinde İşlemler

1.1. Toplama – Çıkarma İşlemi

İki vektörün toplanması, iki vektörü uç uca ekleyerek birinci vektörün başlangıcından ikinci vektörün ucuna doğru yeni bir vektör elde edilmesidir

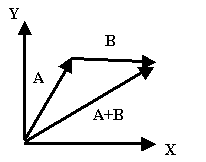
İki vektörün farkı işleminde de aynı şekilde negatif vektörün tersi alınarak toplama işlemi gerçekleşir.

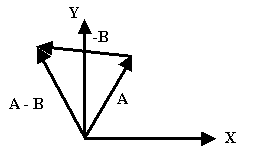
1.2. Vektörün Uzunluğu

Vektörün uzunluğu pisagor bağıntısıyla kolayca bulunabilir.

||v|| = sqrt( x*x + y*y + z*z )

1.3. Vektörü Normalize Etmek

Bir vektörün uzunluğunu 1 birim yapmaya o vektörü Normalize etmek denir. Bunun için vektörün her bir elemanını vektörün uzunluğuna bölmek gerekir.

x = x / ||v||
y = y / ||v||
z = z / ||v||

1.4. Dot İşlemi

Vektörler üzerinde çok önemli bir işlemde Dot işlemidir. Dot işlemi iki vektör arasındaki açısal ilişkiyi gösterir. Aradaki açının cosinüsü ile vektörlerin uzunlukları çarpımına eşittir.

Dot(v1, v2) = cos(a) * ||v1|| * ||v2||

Çarpım işlemi şöyle hesaplanır.

A(ax, ay, az) * B(bx, by, bz) = ax*bx + ay*by + az*bz

yani, Dot(v1, v2) = cos(a) * ||v1|| * ||v2|| = ax*bx + ay*by + az*bz

Buradan anlaşılacağı gibi eğer vektörler normalize edilmişse bu işlemin sonucu aradaki açının cosinüsünü verecektir.

1.5. Cross İşlemi

Vektörler üzerinde çok önemli bir başka işlemde cross işlemidir. Cross işlemi ile iki vektöre dik başka bir vektör bulunur. Bu işlem genelde bir düzlemin normalini bulmak için kullanılır.

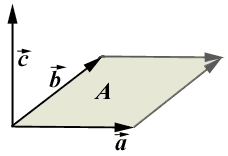
Yukarıdaki şekilde a ve b vektörleri A düzlemi üzerindedir. C vektörü ise bu düzleme dik olan vektördür. Cross(a, b) işlemi ile c vektörü elde edilebilir.

Cross işlemi söyle hesaplanabilir:

c.x = a.y*b.z - b.y*a.z
c.y = a.z*b.x - b.z*a.x
c.z = a.x*b.y - b.x*a.y

C vektörünün yönünü kol kafa yöntemiyle bulabilirsiniz. İlk vektör(a) sağ kolla ikinci vektör(b) sol kolla gösterilirse kafamızın yönü normal vektörünün yönünü gösterir.

Ersin K. :: 2003 :: www.oyunyapimi.org